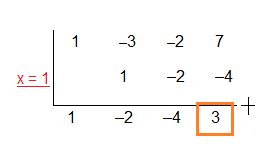Soal - 1

    Hasil dan sisa pembagian suku banyak \(f(x)=x^4-3x^3-2x^2+7\) oleh $g(x)=\frac{1}{2}x-\frac{1}{2}$ berturut-turut adalah ....

    Penyelesaian:

     Pembagi $g(x)=\frac{1}{2}x-\frac{1}{2}$  berarti $x = 1$.

    Dengan menggunakan metode Horner kita peroleh:

    Karena koefisien pembaginya adalah $\frac{1}{2}$ sehingga hasil baginya harus dibagi dengan $\frac{1}{2}$   atau di kali $2$,dengan demikian 

     hasil baginya adalah $$2x^2-4x-8$$

     sisa pembagian adalah $$3$$    

    Soal - 2

    Suku banyak $f(x)$ bersisa $6$ jika dibagi oleh $(x – 2)$ dan bersisa $–3$ jika dibagi oleh $(x + 1)$. Sisa pembagian suku banyak $f(x)$ jika dibagi oleh $x^2-x-2$ adalah ....

    Penyelesaian:

    $f(x)$ bersisa $6$ jika dibagi oleh $(x – 2)$ berarti $f(2) = 6$

   $f(x)$ bersisa $-3$  jika dibagi oleh $(x + 1)$ berarti $f(-1)=-3$ 

    Sementara pembagi $x^2-x-2=(x-2)(x+1)$

    

\[\begin{align*} f(2)&=6\rightarrow 2a+b&=6 .......... (1)\\ f(-1)&=-3\rightarrow -a+b&=-3 .......... (2) \end{align*}\]

dengan mengeliminasi persamaan (1) dan (2) maka diperoleh

\[\frac { \!\begin{aligned} 2a+b &=6\\ -a+b&=-3 \end{aligned} } { \!\begin{aligned} 3a&=9 \\ a&=3 \\ b&=0 \end{aligned} } \ -\]

Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-2$  adalah $3x$

    Soal - 3

    Suku banyak $f(x)$ dibagi oleh $x^2-x$ bersisa $x+1$, jika $f(x)$ dibagi oleh $(x^2 + 2x)$ bersisa $x+5$. Sisa pembagian suku banyak $f(x)$ oleh $x^2+x-2$ adalah ....

    Penyelesaian:

    Pembagi $x^2-x$ bila di faktorkan akan menghasilkan $x^2-x=x(x-1)$   

    $f(x)$ bersisa $x+1$ jika dibagi oleh $x^2-x$ berarti $f(0) = 1$ dan $f(1) = 2$

   Pembagi $x^2+2x$ bila di faktorkan akan menghasilkan $x^2+2x=x(x+2)$   

    $f(x)$ bersisa $x+5$ jika dibagi oleh $x^2+2x$ berarti $f(0) = 5$ dan $f(-2) = 3$

    Sementara pembagi $x^2+x-2=(x+2)(x-1)$

    

\[\begin{align*} f(1)&=2\rightarrow a+b&=2 .......... (1)\\ f(-2)&=3\rightarrow -2a+b&=3 .......... (2) \end{align*}\]

dengan mengeliminasi persamaan (1) dan (2) maka diperoleh

\[\frac { \!\begin{aligned} a+b &=2\\ -2a+b&=3 \end{aligned} } { \!\begin{aligned} 3a&=-1 \\ a&=-\frac{1}{3} \\ b&=\frac{7}{3} \end{aligned} } \ -\]

Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-2$  adalah \[-\frac{1}{3}x+\frac{7}{3}\]