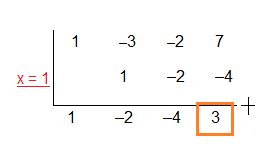Wednesday, November 24, 2021
Monday, November 8, 2021
Monday, October 11, 2021
Wednesday, October 6, 2021
Monday, October 4, 2021
Tuesday, September 21, 2021
Monday, September 20, 2021
Monday, September 13, 2021
Monday, August 16, 2021
Monday, August 2, 2021
Sunday, August 1, 2021
Sunday, July 25, 2021
Sunday, July 18, 2021
Friday, June 4, 2021
Soal - 1
Hasil dan sisa pembagian suku banyak \(f(x)=x^4-3x^3-2x^2+7\) oleh $g(x)=\frac{1}{2}x-\frac{1}{2}$ berturut-turut
adalah ....
Penyelesaian:
Pembagi $g(x)=\frac{1}{2}x-\frac{1}{2}$ berarti $x = 1$.
Dengan menggunakan metode Horner kita peroleh:
Karena koefisien pembaginya adalah $\frac{1}{2}$ sehingga hasil baginya harus dibagi dengan $\frac{1}{2}$ atau di kali $2$,dengan demikian
hasil baginya adalah $$2x^2-4x-8$$
sisa pembagian adalah $$3$$
Soal - 2
Suku banyak $f(x)$
Penyelesaian:
$f(x)$
$f(x)$
Sementara pembagi $x^2-x-2=(x-2)(x+1)$
\[\begin{align*} f(2)&=6\rightarrow 2a+b&=6 .......... (1)\\ f(-1)&=-3\rightarrow -a+b&=-3 .......... (2) \end{align*}\]
dengan mengeliminasi persamaan (1) dan (2) maka diperoleh
\[\frac { \!\begin{aligned} 2a+b &=6\\ -a+b&=-3 \end{aligned} } { \!\begin{aligned} 3a&=9 \\ a&=3 \\ b&=0 \end{aligned} } \ -\]
Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-2$ adalah $3x$
Soal - 3
Suku banyak $f(x)$ dibagi oleh $x^2-x$ bersisa $x+1$, jika $f(x)$ dibagi oleh $(x^2 + 2x)$ bersisa $x+5$. Sisa pembagian suku banyak $f(x)$ oleh $x^2+x-2$
Penyelesaian:
Pembagi $x^2-x$ bila di faktorkan akan menghasilkan $x^2-x=x(x-1)$
$f(x)$
Pembagi $x^2+2x$ bila di faktorkan akan menghasilkan $x^2+2x=x(x+2)$
$f(x)$
Sementara pembagi $x^2+x-2=(x+2)(x-1)$
\[\begin{align*} f(1)&=2\rightarrow a+b&=2 .......... (1)\\ f(-2)&=3\rightarrow -2a+b&=3 .......... (2) \end{align*}\]
dengan mengeliminasi persamaan (1) dan (2) maka diperoleh
\[\frac { \!\begin{aligned} a+b &=2\\ -2a+b&=3 \end{aligned} } { \!\begin{aligned} 3a&=-1 \\ a&=-\frac{1}{3} \\ b&=\frac{7}{3} \end{aligned} } \ -\]
Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-2$ adalah \[-\frac{1}{3}x+\frac{7}{3}\]
Tuesday, May 11, 2021
Bentuk $(a+b)^n$
Buktikan bahwa \[\large \begin{align*} a^2+b^2=(a+b)^2-2ab \end{align*}\]
Penyelesaian:
\[\large \large \begin{align*} (a+b)^2&=a^2+2ab+b^2\\ &=a^2+b^2+2ab\\ (a+b)^2&-2ab=a^2+b^2 \end{align*}\]
Terbukti bahwa \[\large \large \begin{align*}\color{Orange}{ a^2+b^2=(a+b)^2-2ab} \end{align*}\]
Buktikan bahwa \[\large \begin{align*} a^3+b^3=(a+b)^3-3ab(a+b) \end{align*}\]
Penyelesaian:
\[\large \large \begin{align*} (a+b)^3&=a^3+3a^2b+3ab^2+b^3\\ &=a^3+b^3+3a^2b+3ab^2\\ &=a^3+b^3+3ab(a+b)\\ (a+b)^3&-3ab(a+b)=a^3+b^3 \end{align*}\]
Terbukti bahwa \[\large \large \begin{align*}\color{DarkRed}{ a^3+b^3= (a+b)^3-3ab(a+b)}\end{align*}\]
Buktikan bahwa \[\large \begin{align*} a^2+b^2+c^2=(a+b+c)^2-2(ab+ac+bc) \end{align*}\]
Penyelesaian:
\[\large \begin{align*} (a+b+c)^2&=(a+\left (b+c \right )^2\\ &=a^2+2a(b+c)+(b+c)^2\\ &=a^2+2ab+2ac+b^2+2bc+c^2\\ &=a^2+b^2+c^2+2ab+2ac+2bc\\ &=a^2+b^2+c^2+2\left (ab+ac+bc \right )\\ (a+b+c)^2&-2\left (ab+ac+bc \right )=a^2+b^2+c^2\\ \end{align*}\]
Terbukti bahwa \[\large \large \begin{align*} \color{DarkGreen} {a^2+b^2+c^2=(a+b+c)^2-2(ab+ac+bc)}\end{align*}\]
Buktikan bahwa \[\large \begin{align*} a^3+b^3+c^3=(a+b+c)^3-3(a+b)(a+c)(b+c)\\ \end{align*}\]
Penyelesaian:
\[\large \begin{align*} (a+b+c)^3&=(a+(b+c))^3\\ &=a^3+3a^2(b+c)+3a(b+c)^2+(b+c)^3\\ &=a^3+3a^2(b+c)+3a(b+c)^2+b^3+3b^2c+3bc^2+c^3\\ &=a^3+b^3+c^3+3a^2(b+c)+3a(b+c)^2+3bc(b+c)\\ &=a^3+b^3+c^3+3(b+c)\left [a^2+a(b+c)+bc\right ]\\ &=a^3+b^3+c^3+3(b+c)\left [a^2+ab+ac+bc\right ]\\ &=a^3+b^3+c^3+3(b+c)\left [a(a+b)+c(a+b)\right ]\\ &=a^3+b^3+c^3+3(b+c)\left [(a+b)(a+c)\right ]\\ &=a^3+b^3+c^3+3(a+b)(a+c)(b+c)\\ (a+b+c)^3&-3(a+b)(a+c)(b+c)=a^3+b^3+c^3\\ \end{align*}\]
Terbukti bahwa
\[\large \large \begin{align*} \color{DarkOrange}{ {a^3+b^3+c^3=(a+b+c)^3-3(a+b)(a+c)(b+c)}}\\ \end{align*}\]
Suku Banyak
Pembahasan soal Latihan Polinomial
Soal 1
Diketahui suku banyak $f(x)=x^{3}+2x^{2}-3x+p$ jika dibagi oleh $x-1$ memberikan sisa 3. Nilai $p$ adalah ....
Penyelesaian:Sisa pembagian $f(x)$ oleh $x - 1$ adalah 3, berarti $f(1) = 3$
$\begin{array}{rcl}1^{3}+2.1^{2}-3.1+p & = & 3 \\ 1+2-3+p & = & 3 \\ p & = & 3 \end{array}$
Sehingga nilai p adalah 3
Soal 2:
Suku banyak $f(x)$ jika dibagi oleh $x−2$ maka sisanya adalah $3$, sedangkan jika $f(x)$ di bagi oleh $x+1$ memberikan sisa $−3$. Sisa pembagian suku banyak $f(x)$ jika dibagi oleh $x^2-x-2$ adalah ....
Penyelesaian:
Sisa pembagian $f(x)$ oleh $x - 2$ adalah $3$, berarti $f(2) = 3$
Sisa pembagian $f(x)$ oleh $x - 2$ adalah $3$, berarti $f(2) = 3$
Sisa pembagian $f(x)$ oleh $x + 1$ adalah $-3$, berarti $f(-1) = -3$
\[\begin{align*} 2a+b &=3 ................ (1)\\ -a+b&=-3 ............... (2) \end{align*}\]
dengan mengeliminasi persamaan (1) dan (2) maka diperoleh
\[\frac { \!\begin{aligned} 2a+b &=3\\ -a+b&=-3 \end{aligned} } { \!\begin{aligned} 3a&=6 \\ a&=2 \\ b&=-1 \end{aligned} } \ -\]
Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-2$ adalah $2x-1$
Soal 3:
Diketahui $f(x)$ adalah suatu
polinomial. Jika $f(x-2)$ dan $f(x-1)$ dibagi $x-1$ masing-masing memberikan sisa $1$ dan $3$. Apabila $f(x)$ dibagi $x^2 + x$ memberikan sisa ...
Penyelesaian:
Sisa pembagian $f(x-2)$ oleh $x - 1$ adalah $1$, berarti $f(-1) = 1$
Sisa pembagian $f(x-1)$ oleh $x - 1$ adalah $3$, berarti $f(0) = 3$
\[\begin{align*} f(-1)&=1\rightarrow -a+b&=1\\ f(0)&=3\rightarrow b&=3 \end{align*}\]
Dengan mensubstitusi nilai $b=3$ ke $-a+b=1$ diperoleh $a=2$
Dengan demikian, sisa pembagian $f(x)$ oleh $x^2+x$ adalah $2x+3$
Soal 4:
Jika $f(x)$ dibagi dengan $(x − 3)$ sisanya $25$, sedangkan jika dibagi dengan $(x + 2)$ sisanya $5$. Jika $f(x)$ dibagi dengan $x^2-x-6$ maka sisanya adalah ....
Penyelesaian:
Sisa pembagian $f(x)$ oleh $x - 3$ adalah $25$, berarti $f(3) = 25$
Sisa pembagian $f(x)$ oleh $x + 2$ adalah $5$, berarti $f(-2) = 5$
\[\begin{align*} f(3)&=25\rightarrow 3a+b&=25 .......... (1)\\ f(-2)&=5\rightarrow -2a+b&=5 .......... (2) \end{align*}\]
dengan mengeliminasi persamaan (1) dan (2) maka diperoleh
\[\frac { \!\begin{aligned} 3a+b &=25\\ -2a+b&=5 \end{aligned} } { \!\begin{aligned} 5a&=20 \\ a&=4 \\ b&=13 \end{aligned} } \ -\]
Dengan demikian, sisa pembagian $f(x)$ oleh $x^2-x-6$ adalah $4x+13$
Soal 5:
Bila $x+1$ merupakan salah satu faktor suku banyak $x^3+5x^2-kx+3$, maka nilai $k$ adalah ....
Penyelesaian:
Karena $x+1$ merupakan salah satu faktor suku banyak, akibatnya $f(-1)=0$
Dengan mensubstitusi $x=-1$ ke persamaan suku banyak diperoleh
\[\begin{align*} (-1)^3+5.(-1)^2-k(-1)+3&=0\\ -1+5+k+3&=0 \\ k&=-7 \end{align*}\]
Soal 6:
Yang merupakan akar-akar persamaan suku banyak $f(x)=x^4+3x^3-3x^2-11x-6$ adalah ....
Penyelesaian:
Untuk menentukan akar-akar suku banyak digunakan metode horner sebagai berikut
Soal 7:
Salah satu faktor suku banyak $f(x)=x^3+px^2+3x-1$ adalah $x-1$, faktor lainnya adalah ....
Penyelesaian:
Karena $x-1$ merupakan salah satu faktor suku banyak, akibatnya $f(1)=0$
Dengan mensubstitusi $x=1$ ke persamaan suku banyak diperoleh
\[\begin{align*} (1)^3+p.(1)^2+3(1)-1&=0\\ 1+p+3-1&=0 \\ p&=-3 \end{align*}\]
Sehingga $f(x)=x^3-3x^2+3x-1$
Untuk memperoleh akar-akar lainnya, digunakan metode horner
Sehingga faktor yang lainnya adalah $x-1$
Soal 8:
Bila sepasang akar
persamaan suku banyak $f(x) = x^3-2x^2+6x+k$ berlawanan tanda maka
hasil kali ketiga akar
itu adalah ....
Penyelesaian:
Misalkan akar-akar suku banyak tersebut adalah $x_1,x_2$ dan $x_3$
Berdasarkan teorema Vieta
\[\begin{align*} ax^3+ bx^2 + cx + d = 0\\x_1 + x_2 + x_3= -\frac{b}{a}\\ x_1x_2 + x_1x_3 + x_2x_3 = \frac{c}{a}\\ x_1x_2x_3 =-\frac{d}{a} \\ \end{align*}\]
Karena sepasang akar berlawanan berarti $x_1$=$-x_2$
\[\large \begin{align*} x^3 -2x^2 + 6x + k &= 0\\ x_1 + x_2 + x_3&= -\frac{(-2)}{1}\\ x_1-x_1 + x_3 &= 2\\ x_3 &=2 \\ \end{align*}\]
Selanjutnya, menentukan nilai $k$ dengan mensubtitusi \(x_3 =2\) ke persamaan suku banyak:
\(\large \begin{align*} 2^3 -2(2)^2 + 6(2) + k &= 0\\ 8-8+12+k&= 0\\ 12+k &=0\\ k&=-12 \\ \end{align*}\)
Hasil kali ketiga akarnya adalah
\[\large \begin{align*} x_1.x_2.x_3 &= -\frac{d}{a}\\ x_1.x_2.x_3 &=-\frac{k}{a}\\ x_1.x_2.x_3 &=-\frac{(-12)}{1}\\ x_1.x_2.x_3 &=12 \end{align*}\]
Soal 9:
Bila
sepasang akar persamaan suku banyak $f(x)=x^3+kx^2+7x-3$ berkebalikan maka
jumlah ketiga akar itu adalah ....
Penyelesaian:
Misalkan akar-akar suku banyak tersebut adalah $x_1,x_2$ dan $x_3$. Karena sepasang akar Berkebalikan berarti \(x_2=\frac{1}{x_1}\)
Berdasarkan teorema Vieta
\[\large \begin{align*} x^3+kx^2+7x-3&=0\\ x_1 . x_2 . x_3&= 3\\ x_1.\frac{1}{x_1}.x_3&=3 \\ x_3&=3 \end{align*}\]
Selanjutnya, menentukan nilai $k$ dengan mensubtitusi \(x_3 =3\) ke persamaan suku banyak:
\[\large \begin{align*} 3^3 +k(3)^2 + 7(3) -3 &= 0\\ 27+9k+21-3&= 0\\ 9k +45&=0\\9k &=-45\\ k&=-5 \end{align*}\]
Jumlah ketiga akarnya adalah
\[\large \begin{align*} x_1+x_2+x_3 &= -\frac{b}{a}\\ x_1+x_2+x_3 &=-\frac{k}{a}\\ x_1+x_2+x_3 &=-\frac{(-5)}{1}\\ x_1+x_2+x_3 &=5 \end{align*}\]
Soal 10:
Diketahui
sepasang akar-akar suku banyak $f(x)=x^3+px^2-x-2$ adalah berlawanan tanda.
Maka
ketiga akar-akar suku banyak tersebut adalah ....
Penyelesaian:
Misalkan akar-akar suku banyak tersebut adalah $x_1,x_2$ dan $x_3$. Karena sepasang akar berlawanan tanda berarti \(x_1=-{x_2}\)
Berdasarkan teorema Vieta
\[\large \large \begin{align*} x^3+px^2-x-2&=0\\ x_1 + x_2 + x_3&= -\frac{p}{1}\\ x_1-x_1+x_3&=-p \\ x_3&=-p \end{align*}\]
selanjutnya substitusikan nilai \(x_3=-p\) ke persamaan suku banyak, diperoleh \[\large \large \begin{align*} (-p)^3+p(-p)^2-(-p)-2&=0\\ -p^3+p^3+p-2&=0\\ p-2&=0 \\ p&=2 \end{align*}\]
sehingga persamaan suku banyak tersebut adalah \(x^3+2x^2-x-2\)
akar-akarnya ditentukan menggunakan metode horner
Sehingga akar-akar suku banyak tersebut adalah $-2,-1,1$
Soal 11:
Diketahui
suku banyak $f(x)$ bila dibagi oleh $x – 1$ bersisa $-2$, bila dibagi oleh $x +
3$ bersisa $-1$. Sedangkan suku banyak g(x) bila dibagi oleh $x – 1$ bersisa $3$,
bila dibagi $x + 3$ bersisa $2$. Bila $h(x) = f(x).g(x)$ maka sisa pembagian $h(x)$
oleh $x^2 + 2x – 3$ adalah ...
Penyelesaian:
$f(x)$ bila dibagi oleh $x – 1$ bersisa $-2$ berarti $f(1)=-2$
$f(x)$ bila dibagi oleh $x +3$ bersisa $-1$ berarti $f(-3)=-1$
$g(x)$ bila dibagi oleh $x – 1$ bersisa $3$ berarti $g(1)=3$
$g(x)$ bila dibagi oleh $x +3$ bersisa $2$ berarti $g(-3)=2$
karena $h(x) = f(x).g(x)$ berarti \[\begin{align*} h(1) = f(1).g(1)&=(-2)(3)\rightarrow h(1)&=-6\\ h(-3) = f(-3).g(-3)&=(-1)(2)\rightarrow h(-3)&=-2 \end{align*}\]
Sisa pembagian suku banyak tersebut adalah $s(x)=ax+b$
\[\begin{align*} x=1\rightarrow a+b&=-6 .......... (1)\\ x=-3\rightarrow -3a+b&=-2 .......... (2) \end{align*}\]
eliminasi persamaan (1) dan (2)
\[\frac { \!\begin{aligned} a+b &=-6\\ -3a+b &=-2 \end{aligned} } { \!\begin{aligned} 4a &= -4 \\ a&=-1\\ b&=-5 \end{aligned} } \ -\]
Dengan demikian sisa pembagian $h(x)$ oleh $x^2 + 2x – 3$ adalah $-x-5$
Soal 12:
Suku
banyak $x^3+x^2+4x+4$ dapat difaktorkan menjadi $(x+p)(x^2+qx+r)$. Nilai dari $p+q+r$
adalah
....
Penyelesaian:
\[\begin{align*} x^3+x^2+4x+4&=(x+1)(x^2+4) \\ (x+p)(x^2+qx+r)&=(x+1)(x^2+4) \end{align*}\]
dengan kesamaan suku banyak diperoleh $p=1$, $q=0$ dan $r=4$
sehingga \[\begin{align*} p+q+r&=1+0+4\\ &=5 \end{align*}\]
Soal 13:
Banyaknya
akar real dari persamaan polinomial $x^5-x$ adalah ....
Penyelesaian:
\[\begin{align*} x^5-x&=x(x^4-1)\\ &=x(x^2-1)(x^2+1)\\ &=x(x-1)(x+1)(x^2+1) \end{align*}\]
$x^2+1$ tidak memiliki akar real karena diskriminanya < 0, sehingga banyaknya akar real dari persamaan polinomial $x^5-x$ adalah $3$ buah yaitu $-1, 0, 1$
Soal 14:
Suku
banyak $f(x)=x^3-3x^2+px+q$ habis dibagi oleh $x^2+1$. Nilai $p+q = ....$
Penyelesaian:
\[\begin{align*} x^3-3x^2+px+q&=(x^2+1)(x+r)\\ x^3-3x^2+px+q&=x^3+rx^2+x+r\\ \end{align*}\]
dengan kesamaan suku banyak diperoleh \[\begin{align*} r&=-3\\ p&=1\\ q&=r=-3 \end{align*}\]
sehingga \[\begin{align*} p+q&=1-3\\ &=-2\\ \end{align*}\]
Soal 15:
Bila $p, q, r$ merupakan akar-akar suku banyak $f(x)=x^3+2x^2+6x-12$ maka hasil dari
Penyelesaian:
\[\begin{align*} \frac{1}{p}+\frac{1}{q}+\frac{1}{r}&=\frac{qr+pr+pq}{pqr} \\ &=\frac{\frac{c}{a}}{-\frac{d}{a}}\\ &= \frac{6}{12}\\ &= \frac{1}{2} \end{align*}\]
Soal 16:
Akar-akar suku banyak $f(x)=x^3-2x+1$ adalah $x_1,x_2$ dan $x_3$. Nilai dari \(x_1^{3}+x_2^{3}+x_3^{3}=....\)
Penyelesaian:
\[\begin{align*} f(x)=x^3-2x+1=(x-1)(x^2+x-1) \end{align*}\]
Sehingga $x_1=1$ sementara dari $x^2+x-1$ diperoleh $x_2+x_3=-1$ dan $x_2.x_3=-1$, dengan demikian:
\[\begin{align*} x_1^{3}+x_2^{3}+x_3^{3}&=(x_1+x_2+x_3)^{3}-3(x_1+x_2)(x_1+x_3)(x_2+x_3) \\ &=(0)^3-3(1+x_2)(1+x_3)(x_2+x_3)\\ &=0-3(1+x_2+x_3+x_2x_3)(-1) \\ &=-3(1-1-1)(-1)\\ &=-3(-1)(-1)\\ &=-3 \end{align*}\]
Soal 17:
Nilai p yang memenuhi suku banyak \(\begin{align*} f(x)=\frac{x^3+3x^2-px-3}{x^2-1} \end{align*}\) dapat disederhanakan adalah ....
Penyelesaian:
Supaya suku banyak tersebut dapat disederhanakan berarti \[\begin{align*} x^3+3x^2-px-3&=(x^2-1)(x+a)\\ x^3+3x^2-px-3&=x^3+ax^2-x-a \end{align*}\]
dengan kesamaan suku banyak diperoleh $p=1$
Tuesday, April 20, 2021
Thursday, April 1, 2021
Monday, March 15, 2021
Thursday, February 25, 2021
Wednesday, February 24, 2021
Thursday, January 21, 2021
Tuesday, January 19, 2021
Monday, January 18, 2021
Sunday, January 10, 2021
Tuesday, January 5, 2021
Subscribe to:
Posts (Atom)